講座人: 紀友清教授、朱森教授

講座時間：15:00

講座日期：2020-11-09

地點：騰訊會議（ID：401750651 ）

主辦單位：數學與信息科學學院

報告題目一： Power Set of Some Quasinilpotent weighted shifts

報告人:  紀友清教授

報告人簡介：

紀友清，吉林大學教授，博士生導師，長期從事算子理論與算子代數研究，主持多項國家自然科學基金項目及教育部高等學校博士點專項基金等項目，在Trans. Amer. Math.、 J. Funct. Anal.、J.Operator Theory等國內外期刊上發表了重要學術論文。2004年入選教育部新世紀優秀人才支持計劃。

講座簡介：

For a quasinilpotent operator T, write 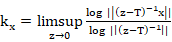 for each nonzero vector x. Set 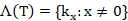$, and call it the power set  of T. This notation was introduced by Douglas and Yang. They showed thatfor 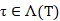, 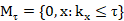$ is a linear subspace invariant under each A commuting with T; hence, if there are two different points  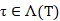such that  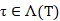are closed, then T has a nontrivial hyperinvariant subspace. It is natural to consider the following questions. Which subsets can be the power set of a quasinilpotent operator? Is  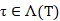closed?  I will talk something about 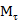and the closeness of.

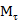報告題目二：隨機Toeplitz代數

報告人:  朱森教授

講座時間：16:30

報告人簡介：

朱森，吉林大學數學學院教授，博士生導師。主持國家自然科學基金青年、面上等項目。近年來主要從事線性算子的復對稱性、隨機理論等方面的研究，在 J. Funct. Anal., J. London Math. Soc., Math. Ann., Trans. AMS 等雜志發表系列論文。

講座簡介：

給定獨立同分布的隨機變量{X_n}_{n\geq 1}, 我們以T表示以{X_n}為權的隨機Hardy移位，其生成的C*代數我們稱為與T相關的隨機Toeplitz代數。本報告將介紹我們關于這一C*代數的若干初步結果，包括理想、表示、穩定秩等。這些結果是經典Toeplitz代數相關結果的隨機版本。